Fraud is often relational. Accounts, devices, transactions, and merchants form networks where suspicious patterns emerge as connections rather than isolated anomalies. Graph neural networks (GNNs) let us directly model these relationships and extract features that traditional tabular models miss. In this post I cover the core ideas of GNNs, practical architectures (GraphSAGE, GAT, GCN), common tasks for fraud detection, feature engineering for graphs, training tips, and production considerations.
Why graphs for fraud detection?
Standard ML models treat each record independently. Fraud, however, is often coordinated: rings of accounts, re-used devices, synthetic identity clusters, and transaction cycles. Graphs let you represent entities as nodes and relationships (transactions, shared addresses, device fingerprints) as edges. This enables:
- Link-aware reasoning — capture influence from neighbors.
- Relational features — centrality, community membership, motif counts.
- Propagation of signals — suspiciousness can diffuse through the network.
GNN building blocks (intuitively)
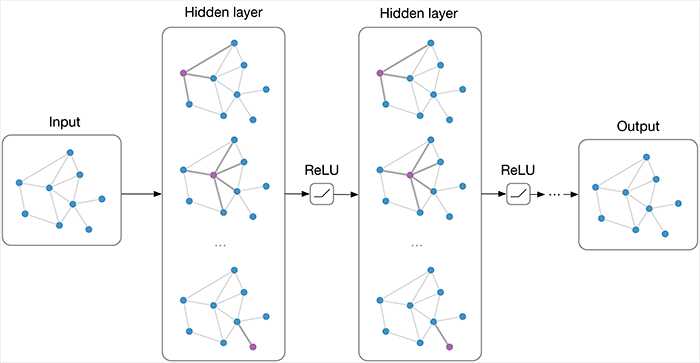
At a high level, a GNN iteratively updates node representations by aggregating information from neighbors. Each layer performs two steps: aggregate neighbor messages, then combine with the node's current state. Stacking layers increases the receptive field.
Common architectures
- GCN (Graph Convolutional Network) — spectral convolution style; simple and fast for homophilic graphs.
- GraphSAGE — samples neighbors and aggregates (mean, LSTM, max); scales to large graphs.
- GAT (Graph Attention Network) — learns attention weights for neighbors; useful when neighbor importance varies.
Fraud detection tasks using GNNs
GNNs can be applied to several problem formulations in fraud:
1. Node classification
Label nodes (accounts, users) as fraudulent vs legitimate. The model uses node features and neighborhood context to predict risk.
2. Link prediction / edge classification
Predict whether a transaction (edge) is fraudulent, or whether a future suspicious link will appear (e.g., account takeover link between device and account).
3. Anomaly detection
Use unsupervised or self-supervised GNNs to learn normal connectivity patterns and flag deviations — for example, unusual hub formation or sudden high-degree changes.
Feature engineering for graphs
Good graph features combine structural signals and domain metadata.
- Node attributes: account age, KYC status, historical fraud score, average transaction amount.
- Edge attributes: transaction amount, timestamp, channel (web/mobile), geo-distance.
- Structural features: degree, PageRank, clustering coefficient, community id (Louvain), motifs (triangles, 4-cycles).
- Temporal features: sliding-window degree growth, burstiness, velocity of transactions.
Practical PyTorch Geometric example (edge classification)
Below is a compact example to illustrate building a graph dataset and an edge classifier using PyTorch Geometric. This is conceptual — adapt data loading and preprocessing to your pipeline.
import torch
import torch.nn.functional as F
from torch_geometric.nn import GraphConv, SAGEConv, GATConv
from torch_geometric.data import HeteroData, DataLoader
# Example: build a simple heterogeneous graph (accounts, devices, transactions)
data = HeteroData()
# node features (n_accounts x d)
data['account'].x = torch.randn(num_accounts, feat_dim)
data['device'].x = torch.randn(num_devices, feat_dim)
# edges: account -> device (uses transaction features as edge attributes)
data['account', 'uses', 'device'].edge_index = edge_index_account_device # 2 x E
data['account', 'uses', 'device'].edge_attr = edge_attr # E x edge_feat_dim
# Simple GraphSAGE-based encoder
class AccountEncoder(torch.nn.Module):
def __init__(self, in_dim, hid_dim):
super().__init__()
self.conv1 = SAGEConv(in_dim, hid_dim)
self.conv2 = SAGEConv(hid_dim, hid_dim)
def forward(self, x, edge_index):
x = F.relu(self.conv1(x, edge_index))
x = F.relu(self.conv2(x, edge_index))
return x
# Edge classifier (concat node embeddings + edge features)
class EdgeClassifier(torch.nn.Module):
def __init__(self, node_dim, edge_feat_dim):
super().__init__()
self.lin = torch.nn.Linear(2*node_dim + edge_feat_dim, 64)
self.out = torch.nn.Linear(64, 1)
def forward(self, src_emb, dst_emb, edge_attr):
h = torch.cat([src_emb, dst_emb, edge_attr], dim=1)
h = F.relu(self.lin(h))
return torch.sigmoid(self.out(h))
# Training loop: compute node embeddings, then classify edges
Scaling to large graphs
Enterprise fraud graphs can have millions of nodes and edges. Strategies to scale:
- Neighborhood sampling (GraphSAGE style) to limit per-batch computation.
- Mini-batch training on subgraphs instead of full-graph propagation.
- Graph partitioning or distributed training frameworks (DGL, PyG with PyTorch Distributed).
- Precompute embeddings periodically for downstream lightweight models (embedding refresh cadence depends on data velocity).
Temporal graphs and streaming data
Fraud evolves over time — accounts connect, devices reappear, new merchants show up. Temporal GNNs and dynamic graph approaches handle this:
- Snapshot-based approach: create time-window graphs and either train across snapshots or use sequence models on embeddings.
- Temporal message passing: models like TGAT and TGN add time-aware attention and memory to handle events.
- Event-based pipelines: ingest transactions as events, update incremental embeddings, and run lightweight classifiers for real-time decisions.
Evaluation and metrics
Evaluation should match the business goal. Common choices:
- AUC / ROC for ranking fraudulent vs legitimate cases.
- Precision at k when manual review resources are limited.
- Detection latency for near real-time use cases.
- Robustness checks — ensure model performance across segments and over time (drift detection).
Interpreting GNNs
Explainability remains important in fraud. Techniques include:
- Node-level attention weights from GAT to see which neighbors influenced the prediction.
- Gradient-based attribution to measure sensitivity to node/edge features.
- Subgraph extraction — identify influential subgraphs and present them to analysts for human review.
Production considerations
Deploying GNNs needs careful engineering:
- Feature store integration. Keep node and edge features accessible with low latency.
- Embedding service. Serve precomputed node embeddings via a scalable service; update periodically or incrementally.
- Real-time scoring. For transaction-time decisions, combine lightweight rules/ML with embedding lookups and a small classifier.
- Monitoring. Track embedding drift, degree distribution changes, and downstream metrics (false positive rate, review burden).
Case study: Detecting synthetic identity rings
Problem: A fraud ring creates many synthetic accounts that share devices, IPs, or addresses to exploit onboarding offers.
Approach used:
- Construct a heterogeneous graph: account, device, email, IP nodes; edges for observed associations.
- Compute structural features (degree, community id) and run a GNN (GraphSAGE) for node classification.
- Rank accounts by model score; perform link analysis for top clusters and present clusters to analysts.
Outcome: The GNN flagged coordinated clusters that were missed by per-account models. Analysts could investigate clusters rather than individual accounts, reducing manual workload and improving recall of coordinated fraud.
Common pitfalls and how to avoid them
- Label leakage. Avoid using features that reflect downstream actions (e.g., a label derived from manual review that used the same signals).
- Imbalanced labels. Use appropriate sampling or loss adjustments; evaluate with precision@k.
- Over-smoothing. Too many GNN layers can make node representations indistinguishable — tune depth carefully.
- Data freshness. For fast-moving fraud, stale embeddings reduce effectiveness — design update cadence accordingly.
Conclusion
Graph neural networks are a powerful tool for fraud detection because they directly model relationships that matter in adversarial settings. The models let you detect coordinated behavior, improve recall of fraud rings, and surface suspicious subgraphs for analyst investigation. The practical challenges are engineering-related: scaling, temporal updates, and integrating embeddings into real-time decisioning. When combined with strong feature engineering, monitoring, and human-in-the-loop processes, GNNs can materially improve fraud detection outcomes.
"In fraud detection, relationships speak louder than isolated signals. Graphs make those relationships usable at scale." – Ashish Gore
If you want, I can produce a compact technical appendix with a runnable PyG example (data simulator + training loop) that you can adapt to your datasets. Or I can create visual diagrams showing the pipeline from event ingestion to embedding service and real-time scoring.